Apolonian Circle Inversion

I was reading some old notes from some math research I did in 2004. I was looking at the Soddy Equation---

(a + b + c + d)^2 = 2(a^2 + b^2 + c^2 + d^2)

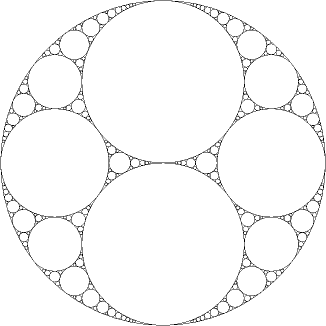
— which relates the curvatures of four kissing circles (see Descartes' theorem). Example of four kissing circles.

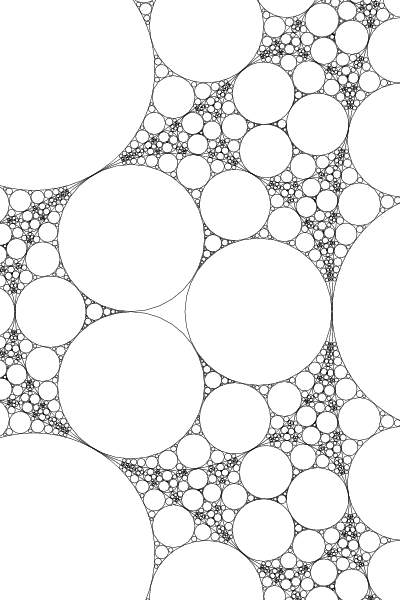
Given three kissing circles, one can find two possible fourth circles (it's a quadratic, right?). This makes a cluster algebra-like thing and graphically makes a Apollonian gasket.

So far no big suprise. This has all been known since Rene Descartes.

* * *

We had an interesting idea. Draw a Apolonian Gasket. For each of the infinite number of circles in the gasket, perform a circle inversion of all the OTHER circles with respect to that circle. Then plot that out. Repeat the process on all the new circles, ad infinitum. You now have an infinite number of circles, topologically dense in R^2, with the property that no two circles intersect in anyway but tangentially.

I never came up with a decent way to program a computer to display such a set.

I called this the Dionysian Gasket.